स्प्लाईन (गणित)

गणित में कई निष्कोण वक्रों (smooth curves) को जोड़कर बने वक्र को स्प्लाइन (Spline) कहते हैं। अतः यह एक पर्याप्त रूप से निष्कोण खण्डश: बहुपद (piecewise polynomial) है। अन्तर्वेशन की समस्याओं में स्प्लाईन अन्तर्वेशन प्रायः बहुपद अन्तर्वेशन (polynomial interpolation) की तुलना में अधिक पसंद किया जाता है क्योंकि यह कम डिग्री के बहुपदो का उपयोग करते हुए भी समान परिणाम देता है। इसके अलावा उच्च डिग्री के उपयोग से बहुपद अन्तर्वेशन में आने वाली रुंग परिघटना (Runge's phenomenon) स्प्लाइन अन्तर्वेशन में नहीं आती।

छः बहुपद खंडों से बनी एक द्विघात स्प्लाईन। इस स्प्लाइन के बिंदु 0 और 1 का भाग एक सरल रेखा है ; बिंदु 1 और 2 के बीच का भाग एक परवलय है जिसका द्वितीय अवकलज = 4 है ; बिंदु 2 और 3 के बीच का खण्ड भी एक परवलय है जिसका द्वितीय अवकलज = - 2 है ; बिन्दु 3 और 4 के बीच का खण्ड एक सरल रेखा है ; बिंदु 4 और 5 बिंदु द्वितीय अवकलज = 6 वाला परवलय है ; बिन्दु 5 और 6 के बीच एक सरल रेखा है।

सात बहुपद खण्डों से निर्मित एक घन स्प्लाईन। पल्स (भौतिकी) लेख में यही स्प्लाइन स्पंद (pulse) को निरूपित करने के लिये प्रयुक्त हुआ है।

ऊपर दर्शाई गयी घन स्प्लाईन का द्वितीय अवकलज (second derivative)

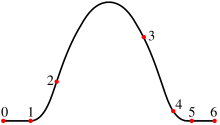
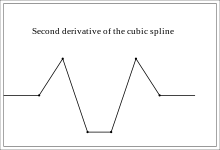
कंप्यूटर ग्राफिक्स में स्प्लाईन का बहुत उपयोग होता है क्योंकि इनका गठन सरल होता है, मूल्यांकन यथार्थ एवं आसान है और यह जटिल आकार को भी इंटरैक्टिव कर्व डिजाईन के माध्यम से सन्निकटीकरण (approximation) करने में सक्षम है। सामान्यतः घन स्प्लाइन (cubic spline) (त्रिघाती स्प्लाईन), विशेष रूप से घन B-spline एवं घन Bézier spline उपयोग में लाए जाते हैं।

परिभाषा

स्प्लाईन एक खंडित बहुपद रियल फंक्शन है।

$S:[a,b]\to \mathbb {R}$

एक अंतराल [a,b] जो की k क्रमांकित एवं विभिन्न उप अंतरालों $[t_{i-1},t_{i}]$ से निर्मित है एवं

$a=t_{0}<t_{1}<\cdots <t_{k-1}<t_{k}=b$.

S को i अंतराल के लिए सीमित करना एक बहुपद है

$P_{i}:[t_{i-1},t_{i}]\to \mathbb {R}$,

ताकि

$S(t)=P_{1}(t){\mbox{, }}t_{0}\leq t<t_{1},$

$S(t)=P_{2}(t){\mbox{, }}t_{1}\leq t<t_{2},$

$\vdots$

$S(t)=P_{k}(t){\mbox{, }}t_{k-1}\leq t\leq t_{k}.$

बहुपद $P_{i}(t)$ का उच्चतम क्रम स्प्लाईन का क्रम् S कहलाता है। यदि सभी उप-अंतराल एक ही अवधि के हैं तब स्प्लाईन uniform कहलाता है अन्यथा वह non-uniform कहलाता है।

हमारा इरादा एक ऐसे बहुपद चुनने का है जो की S की पर्याप्त निर्विघ्नता की गारंटी देता है। विशेष रूप से, n क्रम के स्प्लाईन के लिए S को n-1 क्रम तक आतंरिक बिंदुओं $t_{i}$: सभी $i=1,\dots ,k-1$ और सभी $j\quad 0\leq j\leq n-1$ पर लगातार विभेदित होना जरूरी है।

$P_{i}^{(j)}(t_{i})=P_{i+1}^{(j)}(t_{i})$

बिन्दुओ के बीच प्रक्षेपित घन-स्प्लाईन की व्युत्पत्ति

यह स्प्लाईन के महत्वपूर्ण उपयोगों में से एक है। इसकी कलन विधि Spline interpolation अनुच्छेद में है।

उदाहरण

घंटी के आकार की इरविन-हॉल स्प्लाईन

उपरी स्प्लाईन का द्वितीय व्युत्पन्न

द्विघात स्प्लाईन का सरल उदाहरण (दुसरे क्रम की स्प्लाईन) है

$S(t)={\begin{cases}(t+1)^{2}-1&-2\leq t<0\\1-(t-1)^{2}&0\leq t\leq 2\end{cases}}$

जिसके लिए $S'(0)=2$

घनीय स्प्लाईन का सरल उदाहरण है

$S(t)=\left|t\right|^{3}$

इस रूप में

$S(t)={\begin{cases}t^{3}&t\geq 0\\-t^{3}&t<0\end{cases}}$

और

$S(0)'=\ 0$

$S(0)''=\ 0$

घनीय स्प्लाईन का घंटी के आकार का वक्र बनाने में उपयोग का उदाहरण इरविन-हॉल बहुपद है:

$f_{X}(x)={\begin{cases}{\frac {1}{4}}(x+2)^{3}&-2\leq x\leq -1\\{\frac {1}{4}}\left(3|x|^{3}-6x^{2}+4\right)&-1\leq x\leq 1\\{\frac {1}{4}}(2-x)^{3}&1\leq x\leq 2\end{cases}}$

इतिहास

कंप्यूटर से पहले गड़ना हाथ से की जाती थी। step function जैसे फंक्शन उपयोग किये जाते थे परन्तु बहुपदों को प्राथमिकता दी जाती थी। कंप्यूटर के आने से स्प्लाईन्स ने पहले बहुपदों को प्रतिस्थापित किया और फिर कंप्यूटर ग्राफिक्स में लचीले और सुडोल आकार बनाने के काम में आये.

सामान्यतः यह मन गया है की स्प्लाईन्स का पहला गणितज्ञ सन्दर्भ Schoenberg, के १९४६ के एक पत्र में किया गया जो की शायद पहली जगह थी जहाँ स्प्लाईन शब्द का प्रयोग हुआ। हालांकि मूल विचार विमान और जहाज निर्माण उद्योग से आया था।

इन्हें भी देखें

• स्प्लाइन अन्तर्वेशन
• खण्डशः रैखिक फलन
• वक्र बैठाना (curve fitting)

और पढ़ें

• Stoer; Bulirsch. Introduction to Numerical Analysis. Springer Science+Business Media. पपृ॰ 93–106. आई॰ऍस॰बी॰ऍन॰ 0387904204.
• Chapra, Canale. Numerical Methods for Engineers (5th संस्करण).
• Koehler; Dr. Ralph D. 2D/3D Graphics and Splines - with source code. आई॰ऍस॰बी॰ऍन॰ 978-0759611870.

सिद्धांत

• Cubic Splines Module Prof. John H. Mathews California State University, Fullerton
• Spline Curves, Prof. Donald H. House Clemson University
• An Interactive Introduction to Splines, ibiblio.org
• Introduction to Splines, codeplea.com

एक्सेल फलन (फंक्शन)

• Open source Excel cubic spline User Defined Function
• SRS1 Cubic Spline for Excel - Free Excel cubic spline function (with utility to embed spline function code into any workbook)

ऑनलाइन उपयोगी सामग्री और औजार

• Online Cubic Spline Interpolation Utility
• Learning by Simulations Interactive simulation of various cubic splines
• Symmetrical Spline Curves, an animation by Theodore Gray, The Wolfram Demonstrations Project, 2007.

कंप्यूटर कोड

• Notes, PPT, Mathcad, Maple, Mathematica, Matlab, Holistic Numerical Methods Institute
• various routines, NTCC
• Sisl: Opensource C-library for NURBS, SINTEF
• Closed Bezier Spline, C#, WPF Archived 2011-12-04 at the वेबैक मशीन, Oleg V. Polikarpotchkin
• Bezier Spline from 2D Points, C#, WPF Archived 2011-12-22 at the वेबैक मशीन, Oleg V. Polikarpotchkin