गहराई पहले सर्च

गहराई पहले सर्च या डेप्थ फ़रस्ट सर्च​ (डीएफएस) (Depth First Search) पेड़([Structures]) या ग्राफ डेटा संरचनाओं ([Data Structures])को पार करने या खोज के लिए एक एल्गोरिथ्म है। यह एल्गोरिथ्म रूट नोड(Root Node) पर शुरू होती है और बैकट्रैकिंग से पहले प्रत्येक शाखा के साथ जहां तक ​​संभव हो पड़ताल करती है (ग्राफ़ सर्च मे रूट नोड के रूप में कुछ मनमाने ढंग से नोड का चयन होता है)।

उन्नीसवी शताब्दी में फ्रेंच गणितज्ञ चार्ल्स पियरे ट्रेमेक्स द्वारा भंवरजाल पहेलीयो को हल करने की रणनीति के रूप में गहराई-पहली खोज के एक संस्करण की जांच की गई थी

• 
  Depth-first tree.svg नोड्स का दौरा करने का अनुक्रम

परिभाषा

डीएफएस का [[1]] और [विश्लेषण] इसके आवेदन क्षेत्र के अनुसार भिन्न होता है। सैद्धांतिक कंप्यूटर विज्ञान में, डीएफएस का उपयोग आम तौर पर एक पूरे ग्राफ को पार करने के लिए किया जाता है, और समय लगता है {\ displaystyle ((V V | + + E |)} O (| V | + | E |), रैखिक आकार में ग्राफ का। इन अनुप्रयोगों में यह स्थान विश्लेषण का उपयोग भी करता है {\ displaystyle O (| V |)} O (| V |), सबसे खराब स्थिति में वर्तमान खोज पथ पर ढेरों को संग्रहीत करने मे और पहले से देखे गए कोने का सेट मे। इस प्रकार, इस सेटिंग में, समय और स्थान सीमाएं चौड़ाई-पहली खोज([First Search]) के लिए समान हैं और और इनमें से किसका उपयोग करना है ये विकल्प उनकी जटिलता पर कम निर्भर करता है और दोनो एल्गोरिदम जिन शीर्ष क्रम का उत्पादन करती है उनके गुणो पर अधिक करता है। विशिष्ट डोमेन के संबंध में डीएफएस के अनुप्रयोगों के लिए, जैसे कि आर्टीफ़ीसीयल इन्टेल्लिजेन्स् ([Intelligence]) या वेब-क्रॉलिंग([Crawling]) में समाधान खोजना, ट्रैवर्स किए जाने का ग्राफ अक्सर अपनी संपूर्णता या अनंत यात्रा के लिए बहुत बड़ा होता है।

ऐसे मामलों में,सीमित संसाधनों (जैसे कि मेमोरी या डिस्क स्थान) के कारण खोज केवल एक सीमित गहराई ([depth]) तक की जाती है; आम तौर पर हम विज़िट किए गए वर्सेट्स के संग्रह को अभिलिखित रखने के लिए डेटा संरचनाओं का उपयोग नहीं करते है। जब खोज एक सीमित गहराई तक की जाती है, तो विस्तारित कोनो (vertex) और किनारों (edges) की संख्या के मामले में समय तो रैखिक ही है लेकिन इस प्रकार के डीएफएस की स्पेस जटिलता केवल गहराई सीमा के लिए आनुपातिक है, और इसके परिणामस्वरूप, इसी गहराई की चौड़ाई-पहली खोज की तुलना में बहुत कम जगह लेती है।

उदाहरण

निम्नलिखित ग्राफ के लिए

• 
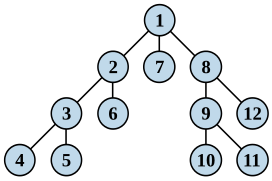
  डीएफ़एस का उदाहरण

A पर शुरू होने वाली एक गहराई-पहली खोज, यह मानते हुए कि दिखाए गए ग्राफ़ में बाएं किनारे दाएँ किनारों से पहले चुने गए हैं, और यह मानकर कि पहले से देखे गए नोड्स में खोज याद रहती है और उन्हें नहीं दोहराएगी (क्योंकि यह एक छोटा ग्राफ़ है), नोड्स का दौरा निम्नलिखित क्रम में:" ए, बी, डी, एफ, ई, सी, जी" करेगा। इस खोज में निकले किनारों को एक ट्रैमॉक्स ट्री([tree]) बनता है, जो कि ग्राफ सिद्धांत([theory]) में महत्वपूर्ण अनुप्रयोगों मे प्रयोग होता है । पहले से देखे गए नोड्स को याद किए बिना उसी खोज को निष्पादित करने से ए, बी, डी, एफ, ई, ए, बी, डी, एफ, ई आदि क्रमों में हमेशा पकड़े जाते है जबकि E C, G नहीं। इस अनंत लूप से बचने के लिए आईटरेटिव डीपनिङ​(Iterative deepening) एक तकनीक है जो कि सभी नोड्स तक पहुन्चती है।

गहराई-पहली खोज का आउटपुट

एक ग्राफ की गहराई-पहली खोज का वर्णन खोज के दौरान पहुन्चे गये कोनो के स्पैनिंग ट्री ([tree]) के संदर्भ में किया जाता है। इस स्पैनिंग ट्री के आधार पर, मूल ग्राफ के किनारों को तीन वर्गों में विभाजित किया जा सकता है: आगे के किनारे, जो पेड़ के एक नोड से उसके वंशज की ओर सन्केत करते है, पीछे के किनारे, जो अपने पूर्वजों में से एक नोड से इंगित करते हैं, और पार किनारों, जो कुछ भी नही करते है। कभी-कभी वो पेड के किनारे जो स्पैनिंग ट्री के होते हैं, उनको आगे के किनारों से अलग से वर्गीकृत किया जाता है । यदि मूल ग्राफ अनिर्दिष्ट है तो इसके सभी किनारे ट्री के किनारे या पीछे के किनारे हैं।

स्यूडोकोड

इनपुट: एक ग्राफ G और G का एक शीर्ष v

आउटपुट: खोजे गए सभी लेबल v से उपलब्ध हैं

डीएफएस का एक पुनरावर्ती कार्यान्वयन

   label v as discovered
   for all directed edges from v to w that are in G.adjacentEdges(v) do
       if vertex w is not labeled as discovered then
           recursively call DFS(G, w)

इस एल्गोरिथ्म द्वारा जिस क्रम में कोने खोजे जाते हैं, उसे लेक्सिकोग्राफिक ऑर्डर कहा जाता है।

जटिल स्थिति में डीएफएस का एक गैर-पुनरावर्ती कार्यान्वयन {\ displaystyle O (! E)}} O (! E)), स्टैक पर डुप्लिकेट वर्टिकल की संभावना के साथ

   let S be a stack
   S.push(v)
   while S is not empty do
       v = S.pop()
       if v is not labeled as discovered then
           label v as discovered
           for all edges from v to w in G.adjacentEdges(v) do 
               S.push(w)

पुनरावृत्त गहराई-पहली खोज का एक अन्य संभावित कार्यान्वयन नोड्स के ढेर के बजाय, नोड के पड़ोसियों की सूची के पुनरावृत्तियों(iterators) के ढेर का उपयोग करता है। यह पुनरावर्ती डीएफएस के रूप में एक ही ट्रैवर्सल पैदा करता है:

   let S be a stack
   S.push(iterator of G.adjacentEdges(v))
   while S is not empty do
       if S.peek().hasNext() then
           w = S.peek().next()
           if w is not labeled as discovered then
               label w as discovered
               S.push(iterator of G.adjacentEdges(w))
       else
           S.pop()

अनुप्रयोग

बिल्डिंग ब्लॉक के रूप में गहराई-पहली खोज का उपयोग करने वाले एल्गोरिदम मे निम्न शामिल हैं:

• जुड़े हुए घटकों को खोजना ([components])
• सामयिक छँटाई ([Sorting])
• 2- (एज या वर्टेक्स) संबंधित घटक द्वारा खोज
• एक ग्राफ के [[2]] का पता लगाना

जटिलता

जॉन रेफ़ द्वारा डीएफएस की कम्प्यूटेशनल जटिलता की जांच की गई । अधिक सटीक रूप से,मान लिया जाये कि एक ग्राफ़ G दिया गया है, और इसमे O = (v1,v2,..., vn) मानक पुनरावर्ती डीएफएस एल्गोरिथ्म द्वारा मान्य पुनरावर्ती डीएफएस एल्गोरिथ्म द्वारा निकाली गई क्रमबद्धता है। इस क्रमबद्धता को लेक्सिकोग्राफिक डेप्थ-फर्स्ट सर्च ऑर्डर कहा जाता है। जॉन रेफ़ ने एक ग्राफ और एक स्रोत के लिये लेक्सोग्राफ़िक गहराई-पहले खोज क्रम की गणना करने की जटिलता पे काम किया। [./Https://en.wikipedia.org/wiki/Decision%20problem समस्या के एक संस्करण] (परीक्षण करना कि क्या इस क्रम में कुछ शीर्ष v से पहले कुछ शीर्ष u होता है) को P Complete कहते है, जो कि समानांतर प्रसंस्करण (Parallel Processing)के लिये एक बहुत बडा एवम कठिन कार्य है