जड़त्वाघूर्णों की सूची

यहाँ पर विभिन्न आकार-प्रकार के पिण्डों के जड़त्वाघूर्ण दिये गये हैं। ज। दत्वाघूर्ण की इकाई की विमा द्रव्यमान × लम्बाई² होती है। नीचे दिये गये व्यंजकों की गणना में यह माना गया है कि घनत्व सर्वत्र समान है।

टिप्पणी: जहाँ कहीं भी अलग से न कहा गया हो, यह माना गया है कि घूर्णन-अक्ष द्रव्यमान केन्द्र से जाता है।

वर्णन	चित्र	जड़त्वाघूर्ण	टिप्पणी
पतला बेलनाकार शेल (shell) जिसके सिरे खुले हैं, त्रिज्या r तथा द्रव्यमान m		$I=mr^{2}\,\!$	शेल की मोटाई को नगण्य (शून्य) माना गया है। यह अगले पिण्ड का एक विशेष दशा है जिसमें r1=r2.
मोटी दिवार वाली खुले सिरों वाली बेलनाकार नली जिसकी अन्त:त्रिज्या r1, वाह्य त्रिज्या r2, लम्बाई h एवं द्रव्यमान m		$I_{z}={\frac {1}{2}}m\left({r_{1}}^{2}+{r_{2}}^{2}\right)$ $I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{2}}^{2}+{r_{1}}^{2}\right)+h^{2}\right]$ or when defining the normalized thickness tn = t/r and letting r = r2, then $I_{z}=mr^{2}\left(1-t_{n}+{\frac {1}{2}}t_{n}^{2}\right)$	घनत्व ρ और उपरोक्त ज्यामिति के साथ $I_{z}={\frac {1}{2}}\pi \rho h\left({r_{2}}^{4}-{r_{1}}^{4}\right)$
r त्रिज्या, h उंचाई, तथा m द्रव्यमान का ठोस बेलन		$I_{z}={\frac {mr^{2}}{2}}\,\!$ $I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)$	This is a special case of the previous object for r1=0.
Thin, solid disk of radius r and mass m		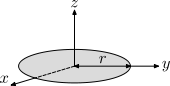$I_{z}={\frac {mr^{2}}{2}}\,\!$ $I_{x}=I_{y}={\frac {mr^{2}}{4}}\,\!$	This is a special case of the previous object for h=0.
Thin circular hoop of radius r and mass m		$I_{z}=mr^{2}\!$ $I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!$	This is a special case of a torus for b=0. (See below.)
Solid sphere of radius r and mass m		$I={\frac {2mr^{2}}{5}}\,\!$	A sphere can be taken to be made up of a stack of infinitesimal thin, solid discs, where the radius differs from 0 to r.
Hollow sphere of radius r and mass m		$I={\frac {2mr^{2}}{3}}\,\!$	Similar to the solid sphere, only this time considering a stack of infinitesimal thin, circular hoops.
Oblate Spheroid of major a, minor b and mass m		$I={\frac {2mb^{2}}{3}}\,\!$	—
Right circular cone with radius r, height h and mass m		$I_{z}={\frac {3}{10}}mr^{2}\,\!$ $I_{x}=I_{y}={\frac {3}{5}}m\left({\frac {r^{2}}{4}}+h^{2}\right)\,\!$	—
Solid cuboid of height h, width w, and depth d, and mass m		$I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)$ $I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)$ $I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)$	For a similarly oriented cube with sides of length $s$, $I_{CM}={\frac {ms^{2}}{6}}\,\!$.
Thin rectangular plane of height h and of width w and mass m		$I_{c}={\frac {m(h^{2}+w^{2})}{12}}\,\!$	—
Thin rectangular plane of height h and of width w and mass m (Axis of rotation at the end of the plate)		$I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!$	—
Rod of length L and mass m		$I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!$	This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the previous object for w=L and h=d=0.
Rod of length L and mass m (Axis of rotation at the end of the rod)		$I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!$	This expression assumes that the rod is an infinitely thin (but rigid) wire.
Torus of tube radius a, cross-sectional radius b and mass m.		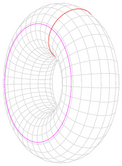About a diameter: ${\frac {1}{8}}\left(4a^{2}+5b^{2}\right)m$ About the vertical axis: $\left(a^{2}+{\frac {3}{4}}b^{2}\right)m$	—
Plane polygon with vertices ${\vec {P}}_{1}$, ${\vec {P}}_{2}$, ${\vec {P}}_{3}$, ..., ${\vec {P}}_{N}$ and mass $m$ uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.		$I={\frac {m}{6}}{\frac {\sum \limits _{n=1}^{N}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|({\vec {P}}_{n+1}^{2}+{\vec {P}}_{n+1}\cdot {\vec {P}}_{n}+{\vec {P}}_{n}^{2})}{\sum \limits _{n=1}^{N}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|}}$	—

इन्हें भी देखें

• समान्तर अक्ष का प्रमेय (Parallel axis theorem)
• क्षेत्राघूर्णों की सूची (List of area moments of inertia)
• जड़त्वाघूर्ण टेंसरों की सूची (List of moment of inertia tensors)