सदस्य:Ripunjoy54/प्रयोगपृष्ठ
प्रतिगमन विश्लेषण

मॉडल में, प्रतिगमन विश्लेषण चर के बीच संबंधों का आकलन करने के लिए एक सांख्यिकीय प्रक्रिया है। जब् यह् ध्यानब् एक आश्रित चर और एक या एक से अधिक स्वतंत्र चर (या 'भविष्यवक्ताओं') के बीच संबंधों पर है, तब् मॉडलिंग और कई चर का विश्लेषण करने के लिए कई तकनीक भी शामिल है। अधिक विशेष रूप से, प्रतिगमन विश्लेषण हमे यह् समझने में मदद करता है कि केसे विशिष्ट निर्भर चर के मूल्य (या 'कसौटी चर') परिवर्तन होता है जब कोइ भी एक स्वतंत्र चर विभिन्न रूप मे हो, जबकि अन्य स्वतंत्र चर निश्चित रूप मे आयोजित हो| सबसे अधिक, प्रतिगमन विश्लेषण स्वतंत्र चर दिया निर्भर चर, की वह् सशर्त उम्मीद का अनुमान करता है - वह है निर्भर चर के औसत मूल्य जब् स्वतंत्र चर तय कर दिया जाए। आम तौर पर कम, ध्यान एक quantile, या स्वतंत्र चर दिया निर्भर चर की सशर्त वितरण के अन्य स्थान पैरामीटर पर है। सभी मामलों में, अनुमान लक्ष्य प्रतिगमन समारोह में बुलाया स्वतंत्र चर के एक समारोह है । प्रतिगमन विश्लेषण में , यह एक संभावना वितरण द्वारा वर्णित किया जा सकता है, जो प्रतिगमन समारोह के आसपास निर्भर चर की भिन्नता को चिह्नित करने के भी हित में है।

प्रतिगमन विश्लेषण व्यापक रूप से भविष्यवाणी और पूर्वानुमान के लिए इस्तेमाल किया जाता है, जहां इसके उपयोग मशीन सीखने के क्षेत्र के साथ पर्याप्त ओवरलैप है। प्रतिगमन विश्लेषण निर्भर चर से संबंधित स्वतंत्र चर के बीच के संबंध को भी समझने के लिए प्रयोग किया जाता है, और इन रिश्तों के रूपों का पता लगाने के लिए प्रयोग् किया जाता है । प्रतिबंधित परिस्थितियों में, प्रतिगमन विश्लेषण स्वतंत्र और आश्रित चर के बीच कारण-रिश्तों को अनुमान करने के लिए भी प्रयोग् किया जा सकता है। हालांकि यह् भ्रम या गलत संबंधों को जन्म दे सकता है, इसलिए सावधानी की सलाह दी जाती है|
प्रतिगमन विश्लेषण को बाहर ले जाने के लिए कई तकनीकों का विकास किया गया है। ऐसे रेखीय प्रतिगमन और साधारण कम से कम वर्गों प्रतिगमन के रूप में परिचित तरीकों पैरामीट्रिक हैं,उस में प्रतिगमन समारोह डेटा से अनुमान किए गए अज्ञात मापदंडों के परिमित संख्या के संदर्भ में परिभाषित किया गया है । Nonparametric प्रतिगमन उन् तकनीक को संदर्भित करता है जो प्रतिगमन समारोह को कार्यों की निर्दिष्ट सेट मे होने की अनुमति देता है, जो अनंत आयामी हो सकता है|
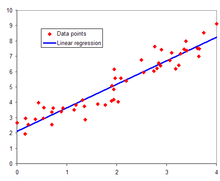
प्रतिगमन विश्लेषण के तरीकों का अभ्यास का प्रदर्शन डेटा पैदा करने की प्रक्रिया के प्रपत्र मे निर्भर करता है, और कैसे यह इस्तेमाल किया जाने वाले प्रतिगमन दृष्टिकोण से संबंधित है। डेटा सृजन प्रक्रिया के असली रूप को आम तौर पर नहीं जान्ने के लिए, प्रतिगमन विश्लेषण अक्सर इस प्रक्रिया के बारे में धारणा बनाने के लिए कुछ हद तक निर्भर करता है। यह् मान्यताओं कभी कभी परीक्षण के योग्य हैं अगर् पर्याप्त मात्रा में डेटा उपलब्ध हो| भविष्यवाणी के लिए प्रतिगमन मॉडल अक्सर उपयोगी होते हैं तब भी जब मान्यताओं मामूली उल्लंघन कर रहे है, हालांकि वे बेहतर प्रदर्शन नहीं कर सकता है| हालांकि, कई अनुप्रयोगों में, विशेष रूप से छोटे प्रभाव या अवलोकन डेटा पर आधारित करणीय के सवालों के साथ, प्रतिगमन तरीकों भ्रामक परिणाम दे सकते हैं । एक संकरा अर्थ में, प्रतिगमन निरंतर प्रतिक्रिया चर का आकलन करने के लिए विशेष रूप से उल्लेख कर सकते हैं, र्गीकरण में प्रयुक्त असतत प्रतिक्रिया चर का विरोध किया| एक सतत उत्पादन चर के मामले अधिक विशेष रूप से संबंधित समस्याओं से अलग करने के रूप में मैट्रिक प्रतिगमन करने के लिए भेजा जा सकता है|
इतिहास कम से कम वर्गों की विधि प्रतिगमन का पहला फार्म था, जो 1805 में Legendre द्वारा और 1809 में गॉस द्वारा प्रकाशित किया गया था| Legendre और गॉस दोनों खगोलीय प्रेक्षण से निर्धारित करने की समस्या को लागू करने की विधि सूर्य के चारों ओर निकायों की कक्षाओं के उपयोग किए गए थे| शब्द " प्रतिगमन " एक जैविक घटना का वर्णन करने के लिए उन्नीसवीं सदी में Francis Galton द्वारा गढ़ा गया था । घटना यह थी कि लंबा पूर्वजों के वंशज की ऊंचाई एक सामान्य औसत ओर नीचे निकासी के लिए करते हैं| Galton के लिए, प्रतिगमन , केवल इस जैविक अर्थ था, लेकिन Udny Yule और कार्ल पियर्सन ने बाद में उनके काम का एक अधिक सामान्य सांख्यिकीय संदर्भ मे विस्तार किया| यूल और पियर्सन के काम में प्रतिक्रिया और व्याख्यात्मक चर के संयुक्त वितरण गाऊसी माना जाता है । आर.ए. फिशर के 1922 और 1925 के काम में यह धारणा कमजोर हो गया था। फिशर मान लिए थे कि प्रतिक्रिया चर की सशर्त वितरण गाऊसी है, लेकिन वह् संयुक्त वितरण नहीं होना चाहिए। इस संबंध में, फिशर का धारणा 1821 के गॉस की तैयार के करीब है। 1950 और 1960 के दशक में , अर्थशास्त्रियों प्रतिगमन गणना करने के लिए विद्युत calculators डेस्क का इस्तेमाल किया था|
प्रतिगमन मॉडल प्रतिगमन मॉडल मे निम्न चर शामिल है: १) अज्ञात पैरामीटर, denoted as β, जो एक अदिश या एक सदिश का प्रतिनिधित्व कर सकता है| २) स्वतंत्र चर, X। ३) आश्रित चर, Y| आवेदन के विभिन्न क्षेत्रों में, निर्भर और स्वतंत्र चर के स्थान पर विभिन्न शब्दावलियों का इस्तेमाल किया जाता हैं| एक प्रतिगमन मॉडल X और β के समारोह को Y से संबंधित करता है। आमतौर पर सन्निकटन E(Y | X) = f(X, β) के रूप मे औपचारिक है| प्रतिगमन विश्लेषण को लागू करने के लिए समारोह के प्रपत्र f को निर्दिष्ट किया जाना चाहिए| कभी कभी इस समारोह का प्रपत्र Y और X के बीच के रिश्ते के ज्ञान पर आधारित है जो डेटा पर भरोसा नहीं करता| अगर ऐसी कोई ज्ञान उपलब्ध नहीं है, f के लिए एक लचीला या सुविधाजनक रूप चुना जाता है|
स्वतंत्र माप की आवश्यक संख्या तीन अज्ञात पैरामीटर, β0 , β1 , और β2 है जो एक प्रतिगमन मॉडल पर विचार करने के लिए है| मान लीजिए कि एक प्रयोगकर्ता स्वतंत्र चर वेक्टर X के बिल्कुल उसी मूल्य पर 10 माप करता है|इस मामले में, प्रतिगमन विश्लेषण तीन अज्ञात मापदंडों के लिए अनुमानित मूल्यों का एक अनूठा सेट देने के लिए विफल रहता है; प्रयोगकर्ता ने पर्याप्त जानकारी प्रदान नहीं किया। सबसे अच्छा एक यह् कर सकते हैं कि औसत मूल्य और आश्रित चर के मानक विचलन का अनुमान लगा है| इसी तरह , X के दो अलग-अलग मूल्यों पर मापने पर दो अज्ञात के साथ एक प्रतिगमन के लिए पर्याप्त डेटा देना होगा, लेकिन तीन या अधिक अज्ञात के लिए देने की जरूरत नहीं है|
निहित मान्यताएं प्रतिगमन विश्लेषण के लिए शास्त्रीय मान्यताओं में शामिल हैं: १) नमूना अनुमान भविष्यवाणी के लिए जनसंख्या का प्रतिनिधि है। २) त्रुटि को व्याख्यात्मक चर पर सशर्त शून्य का एक मतलब के साथ एक यादृच्छिक चर रहा है। ३) स्वतंत्र चर बिना कोई त्रुटि के साथ मापा जाता है| ४)स्वतंत्र चर ( भविष्यवक्ताओं ), रैखिक स्वतंत्र हैं, अर्थात यह दूसरों के एक रेखीय संयोजन के रूप में किसी भी कारक व्यक्त करने के लिए संभव नहीं है। ५) त्रुटि के विचरण टिप्पणियों भर में स्थिर है| यदि नहीं, तो भारित कम से कम वर्गों या अन्य तरीकों के बजाय इस्तेमाल किया जा सकता है। ये वांछनीय गुणों के अधिकारी को कम से कम वर्गों आकलनकर्ता के लिए पर्याप्त शर्तों रहे हैं| विशेष रूप से इन मान्यताओं का मतलब यह् है कि पैरामीटर अनुमान निष्पक्ष होना होगा, संगत, और रैखिक निष्पक्ष आकलनकर्ता की कक्षा में कुशल है। यह नोट के लिए महत्वपूर्ण है कि वास्तविक डेटा शायद ही कभी मान्यताओं को संतुष्ट करता है , अर्थात्वि धि मान्यताओं सच नहीं हैं भले ही प्रयोग किया जाता है| मान्यताओं से भिन्नता कभी कभी (कितनी दूर मॉडल के उपाय उपयोगी होने से है) के रूप में इस्तेमाल किया जा सकता है। इन मान्यताओं के कई और अधिक उन्नत उपचार में ढील दी जा सकती है। सांख्यिकीय विश्लेषण की रिपोर्ट आमतौर पर मॉडल के लिए फिट और उपयोगिता के लिए नमूना डेटा और पद्धति पर परीक्षण के विश्लेषण शामिल हैं।
प्रक्षेप और एक्सट्रपलेशन प्रतिगमन मॉडल X चर के मूल्य दिए जाने पर् Y चर के मूल्यों भविष्यवाणी किया जा सकता हैं। मॉडल-फिटिंग के लिए इस्तेमाल किया डाटासेट में मूल्यों की सीमा के भीतर भविष्यवाणी प्रक्षेप अनौपचारिक रूप में जाना जाता है । डेटा की इस सीमा के बाहर भविष्यवाणी एक्सट्रपलेशन के रूप में जाना जाता है। एक्सट्रपलेशन परफॉर्मिंग प्रतिगमन मान्यताओं पर दृढ़ता से निर्भर करता है। जितना आगे एक्सट्रपलेशन डेटा के बाहर चला जाता है, मॉडल मान्यताओं और नमूना डेटा या सही मूल्यों के बीच मतभेद के कारण विफल करने के लिए और अधिक कमरा है।[1] [2]