फलन

गणित में जब कोई राशि का मान किसी एक या एकाधिक राशियों के मान पर निर्भर करता है तो इस संकल्पना को व्यक्त करने के लिये फलन (function) शब्द का प्रयोग किया जाता है। उदाहरण के लिये किसी ऋण पर चक्रवृद्धि ब्याज की राशि मूलधन, समय एवं ब्याज की दर पर निर्भर करती है; इसलिये गणित की भाषा में कह सकते हैं कि चक्रवृद्धि ब्याज, मूलधन, ब्याज की दर तथा समय का फलन है।

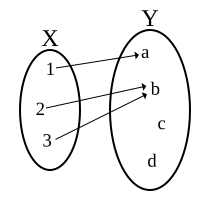
स्पष्ट है कि किसी फलन के साथ दो प्रकार की राशियां सम्बन्धित होती हैं -

एक वे जिनका मान ज्ञात होता है, या दिया गया होता है - इनको स्वतंत्र चर, argument या इन्पुट कहते हैं;
दूसरी वह जिसके मान की गणना करनी होती है, या जिसका मान निकालना होता है -परतंत्र चर, फलन का मान या आउटपुट कहते हैं।

चर राशियों के एक दिये हुए मान के लिये फलन का एक और केवल एक मान होता है।

फलन की संकल्पना (कांसेप्ट), गणित की सबसे मूल एवं महत्वपूर्ण संकल्पनाओं में से एक है। फलन की संकल्पना का विकास एकाएक नहीं हुआ बल्कि इसका विकास कोई दो सौ वर्षों में धीरे-धीरे हुआ और अब भी जारी है। दो राशियों का सम्बन्ध दिखाती एक सूची (टेबल), एक सूत्र (फार्मूला) तथा एल्गोरिद्म आदि फलन के कुछ उदाहरण हैं।

फलन  किसके लिए  परिभाषित होता

फलन की औपचारिक परिभाषा कार्तीय गुणन (Cartesian product) के आधार पर दी जाती है ताकि किसी प्रकार की अनिश्चितता या संदिग्धता न रहे।

दो समुच्चयों X तथा Y का कार्तीय गुणन सभी क्रमित युग्मों (x, y) का समुच्चय है, जहाँ x सदस्य है X का, एवं y सदस्य है Y का। x और y को 'क्रमित युग्म के अवयव' कहा जाता है। X और Y के कार्तीय गुणन को X × Y द्वारा निरूपित किया जाता है।

X से Y पर फलन f कार्तीय गुणनफल X × Y का उपसमुच्चय है, बशर्ते निम्नलिखित शर्तों का पालन होता है

X का प्रत्येक अवयव उपसमुच्चय के एक और केवल एक क्रमित युग्म का प्रथम अवयव है^[1]

दूसरे शब्दों में X के प्रत्येक अवयव x के लिये केवल एक अवयव y ऐसा है कि क्रमित युग्म (x, y) फलन f को पारिभाषित करने वाले उपसमुच्चय का सदस्य है।

फलन का निरूपण

फलन का ग्राफीय निरूपण

{\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}

फलन को भिन्न भिन्न तरीकों से निरूपित (व्यक्त) किया जाता है। इनमें से कुछ तरीके इस प्रकार हैं:

(१) पद के रूप में

x^{2}

(२) समीकरण के रूप में

f(x)=x^{2}

(३) गणना-विधि के रूप में

x\mapsto x^{2}

(४) मानों की तालिका (टेबुल) के रूप में

$x$	1	2	3	4	5	6	…
$y$	1	4	9	16	25	36	…

(५) एक सम्बन्ध के रूप में - जैसा की नीचे क्रमित युग्म के समुच्चय के रूप में दर्शाया गया है।

f=\{(1,1),(2,4),(3,9),(4,16),\ldots \}

(६) दूसरे फलनों के फलन के रूप में (जैसे व्युक्रम या इनवर्स फलन)

:

f=(g^{\prime }\circ h)^{-1}

इन्हें भी देखें

सन्दर्भ

↑ Hamilton, A. G. Numbers, sets, and axioms: the apparatus of mathematics. Cambridge University Press. पृ॰ 83. आई॰ऍस॰बी॰ऍन॰ 0-521-24509-5. मूल से 28 मार्च 2014 को पुरालेखित. अभिगमन तिथि 28 जून 2014.

बाहरी कड़ियाँ

The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
Shodor: Function Flyer, interactive Java applet for graphing and exploring functions.
xFunctions, a Java applet for exploring functions graphically.
Draw Function Graphs, online drawing program for mathematical functions.
Functions from cut-the-knot.
Function at ProvenMath.
Curvas.

[1] Hamilton, A. G. Numbers, sets, and axioms: the apparatus of mathematics. Cambridge University Press. पृ॰ 83. आई॰ऍस॰बी॰ऍन॰ 0-521-24509-5. मूल से 28 मार्च 2014 को पुरालेखित. अभिगमन तिथि 28 जून 2014.

[1]