हेमचन्द्र श्रेणी
गणित में संख्याओं का निम्नलिखित अनुक्रम हेमचंद्र श्रेणी या फिबोनाची श्रेणी (Fibonacci number) कहलाता हैं:


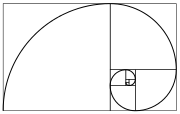
परिभाषा के अनुसार, पहली दो हेमचंद्र संख्याएँ 0 और 1 हैं। इसके बाद आने वाली प्रत्येक संख्या पिछले दो संख्याओं का योग है, (जैसे 2 =1+1, 3 = 1+2; 8 =3+5) । कुछ लोग आरंभिक 0 को छोड़ देते हैं, जिसकी जगह दो 1 के साथ अनुक्रम की शुरूआत की जाती है।
गणितीय सन्दर्भ में, फिबोनाची संख्या के F n अनुक्रम को आवर्तन संबंध द्वारा दर्शाया जा सकता है-
तथा,

फिबोनाची अनुक्रम का नाम पीसा के लियोनार्डो फिबोनाची के नाम पर रखा गया, जो फाइबोनैचि (फिलियस बोनैचियो का संक्षिप्त रूप, "बोनैचियो के बेटे") के नाम से जाने जाते थे। फाइबोनैचि द्वारा लिखित 1202 की पुस्तक लिबर अबेकी ने पश्चिम यूरोपीय गणित में इस अनुक्रम को प्रवर्तित किया, हालांकि पहले ही भारतीय गणित में इस अनुक्रम का वर्णन किया गया है.[1][2]
मूल स्रोत
संपादित करेंफाइबोनैचि अनुक्रम प्राचीन भारत में बहुत प्रसिद्ध था, जहां इसे यूरोप में प्रचलित होने से बहुत समय पहले ही (छन्द-शास्त्र) में लागू किया गया था। इसके विकास का श्रेय पिंगल (200 ई.पू.), विरहांक (6वीं सदी), गोपाल (सन् 1135 ई.), तथा हेमचंद्र (सन् 1150 ई.) को दिया जाता है[3] जिन्होने एल. फिबोनाची (सन् १२०१) के पूर्व ही तथाकथित फिबोनाची संख्याओं तथा उनके निर्माण-विधि का वर्णन किया है। नारायण पंडित (सन् १३५६) ने सामासिका पंक्ति, जिसका एक खास रुप फिबोनाची संख्याएँ हैं, एवं बहुपदी गुणकों के बीच सम्बन्ध स्थापित किया है। (1985 एकेडमिक प्रेस इन्क)
फाइबोनैचि अनुक्रम, n -1 लंबाई के नमूने में S को जोड़ कर, या n -2 लंबाई के नमूने में L को जोड़ कर तैयार किया जाता है; और छंद-शास्त्रियों ने दर्शाया कि n लंबाई के नमूने, अनुक्रम में पिछली दो संख्याओं का योग हैं। डोनाल्ड नुथ ने द आर्ट ऑफ़ कम्प्यूटर प्रोग्रामिंग में इस कार्य की समीक्षा की है।[4]
पश्चिम में, पीसा के लियोनार्डो ने अपने लिबर अबेकी (1202) में फाइबोनैचि के रूप में ज्ञात इस अनुक्रम का अध्ययन किया।[5] उन्होंने एक आदर्श खरगोश की आबादी के विकास (जैविक तौर पर अवास्तविक) पर यह मानते हुए विचार किया कि:
- "शून्य" महीने में, खरगोशों की एक जोड़ी है (खरगोशों के अतिरिक्त जोड़े = 0),
- पहले महीने में, पहली जोड़ी को दूसरी जोड़ी पैदा होती है (खरगोशों के अतिरिक्त जोड़े = 1),
- दूसरे महीने में, खरगोशों के दोनों जोड़े, एक और जोड़े को जन्म देते हैं और पहली जोड़ी मर जाती है (खरगोशों के अतिरिक्त जोड़े = 1),
- तीसरे महीने में, दूसरी जोड़ी और नए दो जोड़ों को कुल तीन नए जोड़े पैदा होते हैं और सबसे वृद्ध जोड़ी मर जाती है (खरगोशों के अतिरिक्त जोड़े = 2),
इसका नियम यह है कि खरगोशों की एक जोड़ी अपने जीवन-काल में 2 जोड़ी पैदा करती है और मर जाती है।
मान लें कि n महीने में आबादी F (n) है। इस समय, केवल वे खरगोश, जो n - 2 महीने में जीवित रहे थे, प्रजननक्षम हैं और संतान पैदा करते हैं, तो F (n − 2) जोड़े मौजूदा आबादी F (n − 1) में जुड़ जाते हैं। इस प्रकार कुल है F (n) = F (n − 1) + F (n − 2).[6]
फाइबोनैचि संख्याओं की सूची
संपादित करेंn = 0, 1, 2, ..., 20 के लिए Fn के रूप में भी सूचित की जाने वाली पहली 21 फाइबोनैचि संख्याएं(sequence A000045 in OEIS) हैं:[7][8]
| F 0 | F 1 | F 2 | F 3 | F 4 | F 5 | F 6 | F 7 | F 8 | F 9 | F 10 | F 11 | F 12 | F 13 | F 14 | F 15 | F 16 | F 17 | F 18 | F 19 | F 20 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 |
आवर्तन संबंध का प्रयोग करते हुए, अनुक्रम ऋणात्मक सूचकांक n तक भी बढ़ाया जा सकता है. परिणाम समीकरण की पूर्ति करता है
इस प्रकार पूरा अनुक्रम है
विभाज्यता गुण
संपादित करेंअनुक्रम की प्रत्येक तीसरी संख्या सम है और आम तौर पर, अनुक्रम की प्रत्येक k वीं संख्या, Fk का गुणज है.इस प्रकार फाइबोनैचि अनुक्रम, एक विभाज्यता अनुक्रम का उदाहरण है. दरअसल, फाइबोनैचि अनुक्रम सुस्पष्ट विभाज्यता गुण को संतुष्ट करता है.
स्वर्णिम अनुपात से संबंध
संपादित करेंपूर्ण सूत्र व्यंजक
संपादित करेंरैखिक आवर्तन द्वारा परिभाषित प्रत्येक अनुक्रम की तरह, फाइबोनैचि संख्या का एक पूर्ण-सूत्र हल है. यह बाइनेट सूत्र के नाम से जाना जाता है, हालांकि उसे पहले अब्राहिम डी मोइव्रे के रूप में जाना गया था:
- जहां , स्वर्णिम अनुपात है
(ध्यान दें कि , जैसा कि उपर्युक्त वर्णित समीकरण से देखा जा सकता है).
फाइबोनैचि प्रत्यावर्तन
स्वर्णिम अनुपात के निर्धारक समीकरण के समान निम्नतः है
जिसे प्रत्यावर्तन के उत्पादक बहुपद के रूप में जाना जाता है.
आगमन द्वारा प्रमाण
संपादित करेंउपर्युक्त समीकरण का कोई मूल का समाधान करता है और द्वारा गुणा करने से निम्न दर्शाता है:
परिभाषा के अनुसार , समीकरण का मूल है और दूसरा मूल है . इसलिए:
और
दोनों तथा ऐसी ज्यामितीय श्रृंखलाएं (for n = 1, 2, 3, ...) हैं, जो फाइबोनैचि प्रत्यावर्तन का समाधान करती हैं. पहली श्रृंखला घातांकी रूप से बढ़ती है; दूसरी, घातांकी रूप से, एकांतर चिह्नों सहित, शून्य की ओर ले जाती है. चूंकि फाइबोनैचि प्रत्यावर्तन रैखिक है, इन दो श्रृंखलाओं के किसी भी रैखिक संयोजन से भी प्रत्यावर्तन का समाधान हो सकता है. ये रैखिक संयोजन, एक दो-आयामी रैखिक वेक्टर अंतर तैयार करते हैं; मूल फाइबोनैचि अनुक्रम इस अंतर में पाया जा सकता है.
रैखिक संयोजनों की श्रृंखलाएं और , a तथा b गुणांकों सहित, निम्न द्वारा परिभाषित की जा सकती हैं
- किसी वास्तविक के लिए
इस प्रकार परिभाषित सभी श्रृंखलाएं फाइबोनैचि प्रत्यावर्तन की पूर्ति करती हैं
जहां अपेक्षा है कि और प्रतिफल और देते हैं, जिसके परिणामस्वरूप वही बाइनेट सूत्र मिलता है, जिससे हमने शुरू किया था. यह दर्शाया गया है कि यह सूत्र फाइबोनैचि प्रत्यावर्तन की पूर्ति करता है. इसके अलावा, एक सुस्पष्ट जांच की जा सकती है:
और
आगमन के मूल प्रश्नों सिद्ध करते हुए, प्रमाणित करते हैं कि
- सभी के लिए
इसलिए, किन्हीं दो प्रारंभिक मूल्यों के लिए, संयोजन को इस तरह पाया जा सकता है कि फलन , अनुक्रम के लिए सटीक पूर्ण सूत्र है.
पूर्णांक द्वारा संगणना
संपादित करेंचूंकि सभी के लिए , अत: संख्या की निकटतम पूर्ण संख्या है | इसलिए यह पूर्णांक द्वारा या निम्न फलन के सन्दर्भ में पाया जा सकता है:
क्रमिक भागफलों की सीमा
संपादित करेंजोहानस केपलर ने टिप्पणी की कि क्रमिक फाइबोनैचि संख्याओं के अनुपात का अभिसरण होता है. उन्होंने लिखा कि "जैसे 5 बटा 8 है, वैसे ही व्यावहारिक तौर पर 8 बटा 13 है और जैसे 8 बटा 13 है, लगभग उसी तरह 13 बटा 21 है" और निष्कर्ष निकाला कि सीमा स्वर्णिम अनुपात सदृश है.[9]
यह अभिसरण 0, 0 को छोड़ कर, चुने गए मूल्यों पर निर्भर नहीं करता है. उदाहरण के लिए, प्रारंभिक मूल्य 19 और 31, अनुक्रम 19, 31, 50, 81, 131, 212, 343, 555 ... आदि को जनित करते हैं. इस अनुक्रम में क्रमिक सीमा का अनुपात, स्वर्णिम अनुपात के प्रति वही अभिसरण दर्शाता है.
प्रमाण
संपादित करेंसंक्षेप में, फाइबोनैचि संख्या लगभग घातीय हैं - , जहां स्थिरांक प्रारंभिक मूल्यों पर निर्भर करता है - जैसे फाइबोनैचि संख्या के लिए गणितीय सूत्र के शेष पद में, n के बढ़ने के साथ-साथ घातीय तौर पर शून्य के निकट हो जाते हैं. अनुपात को लेने पर प्रतिफल होगा
यथानियम, यह हमेशा सुस्पष्ट सूत्र का अनुसरण करे कि किसी वास्तविक के लिए
क्योंकि और इस तरह .
सुनहरे अनुपात के घात का अपघटन
संपादित करेंचूंकि सुनहरा अनुपात निम्न समीकरण की पूर्ति करता है
इस व्यंजक को निम्न घातों के रैखिक संयोजन के रूप में उच्च घातों के अपघटन के लिए प्रयुक्त किया जा सकता है, जिसे बदले में तथा 1 के रैखिक संयोजन तक अपघटित किया जा सकता है. परिणामतः आवर्ती संबंध प्रतिफल में रैखिक गुणांक के रूप में फाइबोनैचि संख्या देते हैं:
यह व्यंजक भी के लिए सही है, यदि फाइबोनैचि अनुक्रम को, फाइबोनैचि नियम का प्रयोग करते हुए ऋणात्मक पूर्णांक तक बढ़ा दिया जाता है.
मैट्रिक्स सूत्र
संपादित करेंरैखिक अंतर समीकरणों की 2-आयामी प्रणाली निम्न है, जो फाइबोनैचि अनुक्रम को परिभाषित करती है
या
मैट्रिक्स A का अभिलक्षणिक मान और है, तथा A के अभिलक्षणिक वेक्टर के तत्व, और का अनुपात और है.
इस मैट्रिक्स का एक -1 सारणिक है और इस तरह यह एक 2×2 एकल-प्रमापीय मैट्रिक्स है. इस गुण को सुनहरे अनुपात के लिए क्रमागत भिन्न के सन्दर्भ में समझा जा सकता है:
फाइबोनैचि संख्याएं के लिए क्रमागत भिन्न के क्रमिक अभिसरकों के अनुपात के रूप में पाए जाते हैं और किसी भी क्रमागत भिन्न के क्रमिक अभिसरकों से बने मैट्रिक्स में +1 या -1 का सारणिक होता है.
मैट्रिक्स प्रतिनिधित्व, फाइबोनैचि संख्या के लिए निम्नलिखित पूर्ण व्यंजक देता है:
इस समीकरण के दोनों ओर के सारणिक को हिसाब में लेने पर प्रतिफल कैसिनी समानिका मिलती है
इसके अतिरिक्त, किसी भी वर्ग मैट्रिक्स के लिए चूंकि , निम्नलिखित समानिकाएं प्राप्त की जा सकती हैं:
विशेष रूप से, के साथ
सूत्रों को प्राप्त करने की एक और पद्धति के लिए दिजक्स्त्रा के "EWD नोट" को देखें.[10]
फाइबोनैचि संख्याओं को पहचानना
संपादित करेंसवाल पैदा हो सकता है कि क्या धनात्मक पूर्णांक एक फाइबोनैचि संख्या है. चूंकि का निकटतम पूर्णांक है, सबसे सीधा, पशु-बल परीक्षण है पहचान
जो सही है, अगर और सिर्फ़ अगर एक फाइबोनैचि संख्या है. इस सूत्र में, पहले चर्चित किसी भी पूर्ण-सूत्र व्यंजक का प्रयोग करते हुए, F(n) की तेजी से गणना की जा सकती है.
वैकल्पिक रूप से, धनात्मक पूर्णांक एक फाइबोनैचि संख्या है अगर और सिर्फ़ अगर या एक पूर्ण वर्ग है.[11]
एक और अधिक परिष्कृत परीक्षण इस तथ्य का उपयोग करता है कि का निरूपण करने वाले क्रमागत भिन्न के अभिसरण, क्रमिक फाइबोनैचि संख्याओं के अनुपात हैं, अर्थात् असमानता
(सह-अभाज्य धनात्मक पूर्णांक , के साथ सही है अगर और सिर्फ़ अगर तथा क्रमिक फाइबोनैचि संख्याएं हैं. इससे यह मानक निकलता है कि एक फाइबोनैचि संख्या है अगर और सिर्फ़ अगर पूर्ण अंतर
में एक धनात्मक पूर्णांक शामिल है.[12]
समानिकाएं
संपादित करें- इस विषय पर अधिक जानकारी हेतु, Young–Fibonacci lattice पर जाएँ
फाइबोनैचि संख्याओं वाली अधिकांश समानिकाएं मिश्रित कोणांकों से उत्पन्न होती हैं. F (n) को 1 तथा 2 के अनुक्रमों की संख्या के रूप में माना जा सकता है, जहां F (0) = 0 के चलन के साथ जिनका योग n -1 बनता है, अर्थात् कोई भी योगफल -1 नहीं हो सकता है और यह कि F (1) = 1, यानि खाली योग 'जोड़ने से' 0 होगा. यहां योज्य का क्रम महत्त्वपूर्ण है. उदाहरण के लिए, 1 + 2 और 2 + 1 दो अलग योग माने जाते हैं और दो बार गिने जाते हैं. इस पर यंग फाइबोनैचि जालक में विस्तार से चर्चा की गई है.
पहली समानिका
संपादित करें- nवीं फाइबोनैचि संख्या, पिछले दो फाइबोनैचि संख्याओं का योग है.
प्रमाण
संपादित करेंहमें सिद्ध करना होगा कि ऊपर प्रस्तुत संयोजक व्याख्या द्वारा निरूपित संख्याओं का अनुक्रम, फाइबोनैचि संख्याओं जैसे ही एकसमान आवर्तन संबंध की पूर्ति करते हैं (और इसलिए वे फाइबोनैचि संख्याओं के समान ही हैं).
F (n + 1) तरीकों से n योगफल सहित 1 और 2 के क्रमित योग बनाने वाला समुच्चय, दो ग़ैर परस्परव्यापी समुच्चयों में विभाजित किया जाए. पहले समुच्चय में वे योगफल हैं, जिनका पहला योज्य 1 है; शेष का योग n − 1 बनता है, अतः पहले समुच्चय में F (n) योगफल हैं.दूसरे समुच्चय में वे योगफल हैं जिनका पहला योज्य 2 है; शेष का योग n − 2 बनता है, अतः दूसरे समुच्चय में F (n − 1) योगफल हैं.पहला योज्य केवल 1 या 2 हो सकता है, अतः ये दोनों समुच्चय, मूल समुच्चय को निःशेष कर देते हैं. इस प्रकार F (n + 1) = F (n) + F (n −1).
दूसरी समानिका
संपादित करें- पहली n फाइबोनैचि संख्या का योग (n + 2) वीं फाइबोनैचि संख्या में से 1 घटा कर बनता है.
प्रमाण
संपादित करेंहम 1 और 2 को n + 1 योगफल देने के तरीक़े से कुछ इस प्रकार गिनते हैं कि कम से कम एक योज्य 2 हो.
पहले जैसे, जब n ≥ 0 हो, तो 1 और 2 को n + 1 में जोड़ने के F (n + 2) तरीक़े हैं. चूंकि केवल एक योगफल n + 1 मौजूद है जो किसी 2 का उपयोग नहीं करता, अर्थात् 1 + ... + 1 (n + 1 पद), हम 1 से F (n + 2) घटाते हैं.
इसी के बराबर, हम योज्य के रूप में 2 की पहली उपस्थिति पर विचार कर सकते हैं. यदि एक योग में, पहला योज्य 2 है, तो n − 1 की गिनती को पूरा करने के लिए वहां F (n) तरीक़े मौजूद हैं. यदि दूसरा योज्य 2 है, लेकिन पहला 1 है, तो n − 2 की गिनती को पूरा करने के लिए वहां F (n − 1) तरीक़े मौजूद हैं. इसी ढंग से आगे बढ़ें. अंततः हम (n + 1) वें योज्य पर विचार करेंगे. यदि यह 2 है लेकिन पिछले सभी योज्य n हैं, तो 0 की गिनती को पूरा करने के लिए F (0) तरीक़े मौजूद हैं. अगर किसी योग में योज्य के रूप में 2 शामिल है, तो ऐसे योज्य की पहली उपस्थिति पहले और (n + 1) वें स्थान के बीच होनी चाहिए. इस प्रकार F (n) + F (n − 1) + ... + F (0) वांछित गिनती देता है.
तीसरी समानिका
संपादित करेंयह समानिका, k विषम है या सम, इस आधार पर F k के लिए थोड़े अलग रूप में है.
- पहली n − 1 फाइबोनैचि संख्याओं का योग, Fj, कुछ इस प्रकार कि j विषम है और (2n) वीं फाइबोनैचि संख्या है.
- पहली n फाइबोनैचि संख्याओं का योग, Fj, कुछ इस प्रकार कि j सम है और (2n + 1) वीं फाइबोनैचि संख्या में से 1 घटा कर है.
प्रमाण
संपादित करेंF 2n के लिए आगमन द्वारा:
इसका मूल उदाहरण F 1 = F 2 हो सकता है.
F 2n +1 के लिए आगमन द्वारा:
इसका मूल उदाहरण F 0 = F 1 − 1 हो सकता है.
वैकल्पिक प्रमाण
संपादित करेंसमानिका 1 के उपयोग द्वारा हम एक अंतर्विद्ध योग रच सकते हैं:
यदि योज्य सम घातांक सहित फाइबोनैचि संख्या है, तो प्रमाण बहुत समान है. दोनों उदाहरणों का योगफल प्रतिफल में समानिका 2 देता है.
चौथी समानिका
संपादित करेंप्रमाण
संपादित करेंइस समानिका को दो चरणों में सिद्ध किया जा सकता है. पहले, हम 1 और 2 को −1, 0, ..., या n + 1 में जोड़ने के तरीक़ों की संख्या को कुछ इस तरह गिनते हैं कि कम से कम एक योज्य 2 हो.
हमारी दूसरी समानिका द्वारा, n + 1 के योग के लिए F (n + 2) − 1 तरीक़े मौजूद हैं; n के योग के लिए F (n + 1) − 1 तरीक़े, ...; और अंततः 1 के योग के लिए F (2) − 1 तरीक़े मौजूद हैं. चूंकि F (1) − 1 = F (0) = 0 है, हम सभी n + 1 योगफल को जोड़ सकते हैं और निम्न को प्राप्त करने के लिए दूसरी समानिका को लागू कर सकते हैं
- [F (n + 2) − 1] + [F (n + 1) − 1] + ...+ [F (2) − 1]
- = [F (n + 2) − 1] + [F (n + 1) − 1] + ...+ [F (2) − 1] + [F (1) − 1] + F (0)
- = F (n + 2) + [F (n + 1) + ... + F (1) + F (0)] − (n + 2)
- = F (n + 2) + [F (n + 3) − 1] − (n + 2)
- = F (n + 2) + F (n + 3) − (n + 3).
- = F (n + 2) + [F (n + 3) − 1] − (n + 2)
- = F (n + 2) + [F (n + 1) + ... + F (1) + F (0)] − (n + 2)
- = [F (n + 2) − 1] + [F (n + 1) − 1] + ...+ [F (2) − 1] + [F (1) − 1] + F (0)
दूसरी ओर, हम दूसरी समानिका से यह देख सकते हैं कि
- F (0) + F (1) + ... + F (n − 1) + F (n) तरीक़े हैं n + 1 योग के लिए;
- F (0) + F (1) + ... + F(n − 1) तरीक़े हैं n योग के लिए;
......
- F (0) तरीक़ा है −1 योग के लिए.
सभी n + 1 योगफलों को जोड़ने पर, हम देखते हैं कि
- (n + 1) F (0) + n F (1) + ... + F(n) तरीक़े हैं −1, 0, ..., या n + 1 योग के लिए.
चूंकि गिनती के दोनों तरीक़े एक ही संख्या को निर्दिष्ट करते हैं, हमारे पास हैं
- (n + 1) F (0) + n F (1) + ... + F (n) = F (n + 2) + F (n + 3) − (n + 3)
अंत में, हम उक्त समानिका को n + 1 बार दूसरी समानिका से घटा कर प्रमाण पूरा करते हैं.
पांचवी समानिका
संपादित करें- पहली n फाइबोनैचि संख्या के वर्गों का योग nवें और (n + 1) वें फाइबोनैचि संख्या का गुणनफल है.
n को दुगुना करने के लिए समानिका
संपादित करेंएक अन्य समानिका
संपादित करेंn के बड़े मूल्यों के लिए Fn की गणना के लिए एक उपयोगी अन्य समानिका है
जिससे k, n और c के अन्य विशिष्ट मूल्यों के लिए अन्य विशिष्ट समानिकाएं निम्न सहित
n और k सभी पूर्णांकों के लिए प्राप्त की जा सकती हैं. दिजक्स्त्रा[10] सूचित करते हैं कि इस प्रकार की द्विगुणक समानिकाएं, n द्वयंकीय आकार के O(log n) लंबे गुणन परिचालनों का उपयोग करते हुए, Fn के परिकलनार्थ प्रयुक्त की जा सकती हैं.प्रत्येक चरण पर, हर गुणन को निष्पादित करने के लिए अपेक्षित परिशुद्धता के अंशों की संख्या दुगुणी हो जाती है, इसलिए निष्पादन अंतिम गुणा द्वारा सीमित होता है; यदि तेज शॉनहेज-स्ट्रासेन गुणन एल्गोरिदम का उपयोग किया जाता है, तो यह O(n log n log log n) अंश परिचालन है. ध्यान दें कि, परिचय में प्रस्तुत ऋणात्मक n सहित फाइबोनैचि संख्या की परिभाषा के साथ, यह सूत्र जब k = 0 हो, तो दोहरा n सूत्र में बदल जाता है.
अन्य समानिकाएं
संपादित करेंअन्य समानिकाओं में शामिल हैं लुकास संख्या के संबंध, जिनमें वही प्रत्यावर्ती गुण हैं, पर L 0 = 2 और L 1 = 1 के साथ शुरू होते हैं. इन गुणों में F 2n = F n L n शामिल हैं.
ऐसी आरोही समानिकाएं भी हैं, जो आपको F n तथा F n+1 से F an+b सूत्र के विभिन्न क़िस्मों की ओर ले जाती हैं; उदाहरण के लिए
- , कैसिनी की समानिका द्वारा.
ये जालक समानयन के उपयोग द्वारा प्रायोगिक तौर पर पाए जा सकते हैं और फाइबोनैचि संख्या के गुणनखंड हेतु विशिष्ट संख्या पकड़ने की छलनी को स्थापित करने के लिए उपयोगी हैं. ऐसे संबंध, आवर्तन संबंधों द्वारा परिभाषित संख्याओं के लिए बहुत ही सामान्य अर्थ में मौजूद हैं, विवरण के लिए पेरिन संख्या के अधीन गुणन सूत्रों का अनुभाग देखें.
घात अनुक्रम
संपादित करेंफाइबोनैचि अनुक्रम का उत्पादक फलन घात अनुक्रम है
इस अनुक्रम में के लिए एक सरल और दिलचस्प पूर्ण सूत्र हल है
को परिभाषित करने वाले अपरिमित योग के प्रत्येक गुणांक के विस्तार के लिए, फाइबोनैचि आवर्तन के उपयोग द्वारा इस हल को सिद्ध किया जा सकता है:
के लिए समीकरण हल करने से परिणाम में पूर्ण सूत्र समाधान मिलता है.
विशेष रूप से, गणित की पहेलियों की क़िताबों में असाधारण मूल्य [15] या अधिक सामान्यतः
सभी पूर्णांकों के लिए पाया जाता है
इसके विपरीत,
व्युत्क्रम योगफल
संपादित करेंकभी-कभी व्युत्क्रम फाइबोनैचि संख्या पर पूर्णांक योगफल का थीटा फलन के सन्दर्भ में मान निकाला जा सकता है. उदाहरण के लिए, हम हर विषम-घातांकी फाइबोनैचि संख्या के योग को निम्नतः लिख सकते हैं
और वर्गाकार व्युत्क्रम फाइबोनैचि संख्या के योग को निम्न रूप में
अगर हम पहले योग में प्रत्येक फाइबोनैचि संख्या के साथ 1 जोड़ दें, तो वहां भी पूर्ण सूत्र होगा
और वर्गाकार फाइबोनैचि संख्या का अच्छा वर्गीकृत योग है, जो सुनहरे अनुपात का व्युत्क्रम देता है,
इस तरह के परिणाम देखने में सही प्रतीत होते हैं कि व्युत्क्रम फाइबोनैचि संख्या के साधारण योग के लिए एक पूर्ण सूत्र पाया जा सकता है, लेकिन अभी तक ऐसा कोई ज्ञात नहीं हुआ है. उसके बावजूद, व्युत्क्रम फाइबोनैचि स्थिरांक
रिचर्ड आन्द्रे-जियानिन द्वारा अपरिमेय साबित किया गया है.
अभाज्य संख्या और विभाज्यता
संपादित करेंफाइबोनैचि अभाज्य संख्या
संपादित करेंफाइबोनैचि अभाज्य संख्या, एक ऐसी फाइबोनैचि संख्या है, जो अभाज्य है.(sequence A005478 in OEIS) पहले कुछ हैं:
- 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ...
हज़ारों अंकों के साथ फाइबोनैचि अभाज्य संख्या पाई गई हैं, लेकिन यह ज्ञात नहीं है कि क्या कई अपरिमित संख्याएं मौजूद हैं.[16] उन सबमें एक अभाज्य घातांक होना चाहिए, सिवाय F 4 = 3.
F kn को F n से विभाजित किया जा सकता है और इसलिए मनमाने ढंग से कई संयुक्त संख्या प्रचलन में होने के कारण, संयुक्त फाइबोनैचि संख्या भी मनमाने ढंग से प्रचलन में हैं.
1, 8 और 144 के अपवाद सहित (F 1 = F 2, F 6 and F 12) प्रत्येक फाइबोनैचि संख्या का एक अभाज्य गुणक है, जो कि किसी छोटे फाइबोनैचि संख्या (कारमाइकेल प्रमेय) का गुणक नहीं है.
केवल 144 नगण्येतर वर्ग फाइबोनैचि संख्या है.[17] एट्टिला पेथो ने 2001 में साबित[18] किया कि केवल सीमित कई परिपूर्ण घात फाइबोनैचि संख्या मौजूद हैं. 2006 में, वाई. ब्यूगॉड, एम. मिग्नोट और एस. सिकसेक ने साबित किया कि केवल 8 और 144, नगण्येतर परिपूर्ण घात हैं.[19]
F 6 = 8 से महत्तर कोई फाइबोनैचि संख्या, अभाज्य संख्या से न तो एक अधिक या एक कम है.[20]
कोई क्रमिक तीन फाइबोनैचि संख्या, एक समय में दो को लेते हुए, आनुपातिक अभाज्य संख्या रही हैं: अर्थात्,
- gcd(F n , F n+1 = gcd(F n , F n+2 ) = 1.
और सामान्यतः,
फाइबोनैचि संख्याओं के अभाज्य भाजक
संपादित करेंफाइबोनैचि संख्याओं की अभाज्य p द्वारा विभाज्यता लीजेन्ड्रे संकेत से संबंधित है जिसका निम्नतः मान निकाला जाता है:
अगर p एक अभाज्य संख्या है, तो [23][24]
उदाहरण के लिए,
यह ज्ञात नहीं है कि कोई अभाज्य p ऐसे मौजूद है कि इस तरह की अभाज्य संख्याओं को (यदि कोई हो तो) वाल-सन-सन अभाज्य संख्या कहा जाएगा.
इसके अलावा, अगर p ≠ 5 एक विषम अभाज्य संख्या है, तो:[25]
सभी मामलों के उदाहरण:
विषम n के लिए, F n के सभी विषम अभाज्य भाजक हैं ≡ 1 (mod 4), जो यह सूचित करते हैं कि F n के (विषम अभाज्य भाजकों के गुणनफल के रूप में) सभी विषम भाजक हैं ≡ 1 (mod 4).[26][27]
उदाहरण के लिए,
F 1 = 1, F 3 = 2, F 5 = 5, F 7 = 13, F 9 = 34 = 2×17, F 11 = 89, F 13 = 233, F 15 = 610 = 2×5×61
11 से विभाज्यता
संपादित करें
उदाहरण के लिए, let n = 1:
F 1 + F 2 + ... + F 10 = 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143 = 11×13
n = 2:
F2+F3+...+F11 = 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 = 231 = 11×21
n = 3:
F3+F4+...+F12 = 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 + 144= 374 = 11×34
वस्तुतः, समानिका न केवल धनात्मक, बल्कि सभी n पूर्णांकों के लिए सही है:
n = 0:
F0+F1+...+F9 = 0 + 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 = 88 = 11×8
n = −1:
F−1+F0+...+F8 = 1 + 0 + 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 = 55 = 11×5
n = −2:
F−2+F−1+F0+...+F7 = −1 + 1 + 0 + 1 + 1 + 2 + 3 + 5 + 8 + 13 = 33 = 11×3
आवर्तक सापेक्ष n
संपादित करेंयह आसानी से देखा जा सकता है कि अगर फाइबोनैचि अनुक्रम की इकाइयों ने mod n लिया है, तो अधिक से अधिक n 2 आवर्तन सहित परिणामी अनुक्रम आवर्तक होनी चाहिए. विभिन्न n सूत्र, तथाकथित पिसानो आवर्तन के लिए आवर्तनों की विस्तार(sequence A001175 in OEIS). सामान्य तौर पर पिसानो आवर्तनों का निर्धारण एक खुली समस्या है,[तथ्य वांछित] हालांकि किसी विशेष n के लिए इसे चक्र संसूचन के उदाहरण के रूप में हल किया जा सकता.
सम त्रिकोण
संपादित करें5 के साथ शुरू होते हुए, हर दूसरा फाइबोनैचि संख्या पूर्णांक भुजाओं सहित सम त्रिकोण के कर्ण की लंबाई है, या दूसरे शब्दों में कहें, पैथागोरियन त्रिगुण में सबसे बड़ी संख्या. इस त्रिकोण के लंबे पाद की लंबाई, त्रिकोण की इस श्रृंखला में पिछले त्रिकोण की तीन भुजाओं के योग के बराबर है और छोटा पाद पूर्ववर्ती हिसाब में न ली गई फाइबोनैचि संख्या और पूर्ववर्ती त्रिकोण के छोटे पाद के बीच के अंतर के बराबर है.
इस अनुक्रम में पहले त्रिकोण की भुजाएं लंबाई में 5, 4 और 3 है. 8 को छोड़ते हुए, अगले त्रिकोण की भुजाएं लंबाई में 13, 12 (5 + 4 + 3) और 5 (8-3) है. 21 को छोड़ते हुए, अगले त्रिकोण की भुजाएं लंबाई में 34, 30 (13 + 12 + 5) और 16 (21-5) है. इस अनुक्रम अनिश्चित रूप से जारी रहता है. त्रिकोण की भुजाएं a, b, c सीधे परिकलित की जा सकती हैं:
ये सूत्र सभी n के लिए को हल करते हैं, लेकिन वे केवल त्रिकोण की भुजाओं का निरूपण करते हैं, जब हो.
एक अलग तरीक़े से पैथागोरियन त्रिगुण को जनित करने के लिए, कोई चार क्रमिक फाइबोनैचि संख्याएं F n , F n +1, F n +2 और F n +3 भी प्रयुक्त की जा सकती हैं.
उदाहरण 1: मान लें फाइबोनैचि संख्याएं 1, 2, 3 और 5 हैं. तब:
उदाहरण 2: मान लें फाइबोनैचि संख्याएं 8, 13, 21 और 34 हैं. तब:
फाइबोनैचि संख्याओं का परिमाण
संपादित करेंचूंकि के लिए उपगामी है, में अंकों की संख्या के प्रति उपगामी है.परिणामतः, प्रत्येक पूर्णांक के लिए, d दशमलव अंकों के साथ 4 या 5 फाइबोनैचि संख्याएं मौजूद हैं.
और सामान्यतः, आधार निरूपण में, में अंकों की संख्या के प्रति उपगामी है.
अनुप्रयोग
संपादित करेंयूक्लिड एल्गोरिदम के चालू समय विश्लेषण में, दो पूर्णांकों के महत्तम उभयनिष्ठ भाजक के निर्धारण के लिए फाइबोनैचि संख्याएं महत्वपूर्ण हैं: इस एल्गोरिदम के लिए सबसे ख़राब समस्या का निवेश क्रमिक फाइबोनैचि संख्याओं की जोड़ी है.[28]
यूरी मतियासेविच यह दर्शा सके कि फाइबोनैचि संख्याओं को डायो फंटाइन समीकरण से परिभाषित किया जा सकता है, जिसने हिल्बर्ट की दसवीं समस्या के उनके मूल समाधान को प्रेरित किया.
फाइबोनैचि संख्याएं, पास्कल त्रिकोण और लोज़ानिक त्रिकोण में "उथले" विकर्णों के योग में होती हैं. (देखें "द्विपद गुणांक"). (वे अधिक स्पष्ट रूप से होसोया त्रिकोण में होती हैं).
हर धनात्मक पूर्णांक को इस तरह से एक या अधिक पृथक् फाइबोनैचि संख्याओं के योग के रूप में एक अनोखे तरीक़े से लिखा जा सकता है, कि योग में कोई दो क्रमिक फाइबोनैचि संख्याएं शामिल ना हों. यह ज़ेकेनडोर्फ़ प्रमेय के रूप में जाना जाता है और फाइबोनैचि संख्याओं का योग जो इन नियमों की पूर्ति करता है, ज़ेकेनडोर्फ़ निरूपण कहलाता है.
वित्तीय बाज़ारों में भी फाइबोनैचि संख्याओं और सिद्धांत का प्रयोग किया जाता है. यह व्यापार एल्गोरिदम, अनुप्रयोगों और योजनाओं में प्रयुक्त होता है. कुछ विशिष्ट प्रकारों में शामिल हैं: फाइबोनैचि फैन, फाइबोनैचि आर्क, फाइबोनैचि रिट्रेसमेंट और फाइबोनैचि टाइम एक्सटेंशन.[तथ्य वांछित]
फाइबोनैचि संख्या कुछ कृत्रिम-यादृच्छिक संख्या जनित्रों द्वारा प्रयुक्त होता है.
फाइबोनैचि संख्याओं को मर्ज सॉर्ट एल्गोरिदम के बहुकलीय संस्करण में प्रयुक्त किया जाता है, जिसमें एक ना छांटी गई सूची को दो सूचियों में विभाजित किया जाता है, जिनकी लंबाई अनुक्रमिक फाइबोनैचि संख्याओं के अनुरूप है - जहां सूची को ऐसे विभाजित किया जाता है कि दोनों भागों की लंबाई समुचित अनुपात φ में हैं. द आर्ट ऑफ़ कम्प्यूटर प्रोग्रामिंग में बहुकलीय मर्ज सार्ट के एक टेप-ड्राइव कार्यान्वयन को वर्णित किया गया है.
फाइबोनैचि संख्याएं, फाइबोनैचि ढेर डाटा संरचना के विश्लेषण में आती हैं.
फाइबोनैचि घन, फाइबोनैचि संख्याओं के कटान-बिंदुओं सहित अनिर्दिष्ट ग्राफ़ है, जिसे समानांतर कंप्यूटिंग के लिए नेटवर्क टोपॉलोजी के रूप में प्रस्तावित किया गया है.
फाइबोनैचि खोज तकनीक नामक एकविमितीय अनुकूलन पद्धति फाइबोनैचि संख्याओं का उपयोग करती है.[29]
फाइबोनैचि संख्या अनुक्रम का उपयोग, अमिगा कंप्यूटरों पर प्रयुक्त IFF 8SVX ऑडियो फ़ाइल फ़ार्मेट में वैकल्पिक ह्रासमान संपीड़न के लिए होता है.संख्या अनुक्रम, लॉगरिदमिक पद्धतियों के समान ही मूल ऑडियो तरंग से शोर को कम करती है जैसे μ-नियम.[30][31]
संगीत में, कभी-कभी फाइबोनैचि संख्याओं का प्रयोग समस्वर निर्धारित करने के लिए होता हैं और दृश्य कला के समान, सामग्री या आवश्यक तत्वों की लंबाई या आकार के निर्धारण के लिए होता है. आम तौर पर यह माना गया है कि बेला बारतोक के म्यूज़िक फ़ॉर स्ट्रिंग्स, परकशन, एंड सेलेस्टा की प्रथम लय फाइबोनैचि संख्याओं के उपयोग से संरचित थी.
चूंकि मील से किलोमीटर के रूपांतरण कारक में 1.609344 सुनहरे अनुपात (φ चिह्नित) के क़रीब है, फाइबोनैचि संख्या के योग में मील की दूरी का अपघटन, लगभग किलोमीटर योग बन जाता है जब फाइबोनैचि संख्याओं को उनके उत्तरवर्तियों द्वारा प्रतिस्थापित किया जाता है.इस विधि से सुनहरे अनुपात के आधार φ के स्थानांतरण में मूलांक 2 संख्या सूचक के बराबर होता है.किलोमीटर से मील में बदलने के लिए, इसके बदले फाइबोनैचि अनुक्रम के नीचे सूचक को खिसकाएं.[32][33][34]
प्रकृति में फाइबोनैचि संख्याएं
संपादित करेंफाइबोनैचि अनुक्रम, दो क्रमिक फाइबोनैचि संख्याओं में, जैविक दृश्यों में दिखाई देते हैं,[35] जैसे पेड़ों में शाखाएं, डंठल पर पत्तियों की व्यवस्था, अनानास की फलिकाएं,[36] एक न मुड़ने वाले फर्न आर्टिचोक का फूल, तथा देवदार शंकु की व्यवस्था.[37] इसके अलावा, प्रकृति के कई लोकप्रिय स्रोतों में फाइबोनैचि संख्याओं या सुवर्ण खंडों के जैसे-तैसे प्रमाणित, यथा खरगोश के प्रजनन, सीपियों के सर्पिल घेरे और लहरों के वक्र से संबंधित दावे मौजूद हैं. [तथ्य वांछित] फाइबोनैचि संख्याएं, मधुमक्खी के वंश-वृक्ष में भी पाई जाती हैं.[38]
प्रेज़ेमिसला पुरुसिंक्विज़ ने इस विचार को आगे बढ़ाया कि वास्तविक उदाहरणों को अंशतः मुक्त समूहों के कतिपय बीजगणितीय प्रतिबंधों की अभिव्यक्ति के रूप में समझा जा सकता है, विशेषतः कुछ लिंडेनमेयर व्याकरण के रूप में.[39]
1979 में एच. वोगेल द्वारा सूरजमुखी के शीर्ष पर पुष्पक की रचना का नमूना प्रस्तावित किया गया.[40] इसका सूत्र है
जहां n पुष्पक का सूचकांक है और c एक निरंतर आरोही गुणक है; इस प्रकार पुष्पक फरमैट के सर्पिल पर स्थित होते हैं. विचलन कोण, 137.51 ° के सन्निकट, स्वर्णिम कोण है, जो वृत्त को सुनहरे अनुपात में बांटता है. क्योंकि यह अनुपात अपरिमेय है, किसी पुष्पक के बग़ल में, केंद्र से बिल्कुल उसी कोण पर कोई और नहीं होता, तो पुष्पक कुशलतापूर्वक एक साथ ठसाठस भर जाते हैं. क्योंकि स्वर्णिम अनुपात के तर्कसंगत सन्निकटन का सूत्र है F (j):F (j + 1), पुष्पक संख्या n के निकटतम पड़ोस में सूचकांक, केंद्र से दूरी r पर आधारित j के लिए n ± F (j) पर है. यह अक्सर कहा जाता है कि सूरजमुखी और इसी तरह की व्यवस्थाओं में 55 घुमाव केवल एक ही दिशा में हैं और 89 अन्य दिशा में (या निकटवर्ती फाइबोनैचि संख्या की कोई अन्य जोड़ी), लेकिन यह केवल एक व्यास के क्षेत्र, विशेषकर सबसे बाहरी और इस तरह सहज रूप से दृश्य के लिए सही है. [41]
मधुमक्खी वंशक्रम कूट
संपादित करेंफाइबोनैचि संख्या, निम्नलिखित नियमों के अनुसार, आदर्श रूप से देखी जाने वाली मधुमक्खियों की आबादी के प्रजनन वर्णन में भी दिखाई देते हैं:
- यदि बिना संसर्ग के एक मादा अंडा देती है, तो उसमें से नर निकलता है.
- यदि, फिर भी, एक अंडा नर द्वारा निषेचित किया गया है, तो उसमें से मादा निकलेगी.
इस प्रकार, नर मक्खी के हमेशा एक जनक होंगे और मादा मक्खी के दो.
यदि कोई किसी नर मधुमक्खी (1 मधुमक्खी) के वंश के विकास को खोजें, तो उसकी 1 मादा जनक (1 मधुमक्खी) होगी. मादा के 2 जनक होंगे, एक मादा और एक नर (2 मधुमक्खियां). मादा के दो जनक, एक नर और एक मादा और नर के एक मादा (3 मधुमक्खियां) होंगी. उन दो मादाओं में प्रत्येक के दो जनक थे और नर के एक (5 मधुमक्खियां). जनकों की संख्या का यह अनुक्रम फाइबोनैचि अनुक्रम है.[42]
यह एक आदर्श रूप है जिसमें वास्तविक मधुमक्खी वंशक्रम का वर्णन नहीं है. वास्तव में, विशिष्ट मधुमक्खी के कुछ पूर्वज हमेशा बहन या भाई होंगे, इस प्रकार पृथक् माता-पिता की वंश परंपरा को तोड़ते हैं.
लोकप्रिय संस्कृति
संपादित करेंसामान्यीकरण
संपादित करेंफाइबोनैचि अनुक्रम को कई मायनों में सामान्यीकृत किया गया है. इनमें शामिल हैं:
- नेगाफाइबोनैचि संख्याएं बनाने के लिए ऋणात्मक पूर्णांकों के घातांक का सामान्यीकरण.
- बाइनेट सूत्र के संशोधन का उपयोग करते हुए घातांक का वास्तविक संख्या में सामान्यीकरण.[14]
- अन्य पूर्णांकों के साथ शुरूआत. लुकास संख्या में L 1 = 1, L 2 = 3, and Ln = L n −1 + L n −2 है.सभी संयुक्त संख्या वाले अनुक्रम को जनित करने के लिए अभाज्यसंख्या-मुक्त अनुक्रम अन्य प्रारंभिक अंकों के साथ फाइबोनैचि प्रत्यावर्तन का उपयोग करते हैं.
- संख्या को पूर्ववर्ती 2 संख्याओं का रैखिक फलन (योग के अलावा) बने रहने देना. पेल संख्याओं में P n = 2P n – 1 + P n – 2 हैं.
- निकटतम पूर्ववर्ती संख्या को न जोड़ना. पैडोवन अनुक्रम और पेरिन संख्या में P(n) = P(n – 2) + P(n – 3) हैं.
- 3 संख्या (ट्रिबोनैचि संख्या), 4 संख्या (टेट्रानैचि संख्या), या और अधिक जोड़ कर अगली संख्या जनित करना.
- पूर्णांकों के अलावा अन्य अंशों को जोड़ना, उदाहरणार्थ फलनक या सूत्र - एक आवश्यक उदाहरण है फाइबोनैचि बहुपद.
इन्हें भी देखें
संपादित करें| विकिपुस्तक पर Fibonacci number program से सम्बन्धित एक किताब है। |
- लॉगरिदमिक घुमाव
- द फाइबोनैचि एसोसिएशन
- फाइबोनैचि क्वार्टरली - फाइबोनैचि संख्या के अध्ययन को समर्पित एक अकादमिक पत्रिका
- नेगाफाइबोनैची संख्या
- लुकास संख्या
- स्वर्णिम अनुपात
- फाइबोनैचि शब्द
नोट
संपादित करें- ↑ परमानंद सिंह. "आचार्य हेमचंद्र और (तथाकथित) फाइबोनैचि संख्या". Math. सं. सीवान, 20 (1) :28-30, 1986. ISSN 0047-6269]
- ↑ परमानंद सिंह, "प्राचीन और मध्ययुगीन भारत में तथाकथित फाइबोनैचि संख्याएं" हिस्टोरिया मैथमैटिका 12 (3), 229-44, 1985.
- ↑ Susantha Goonatilake (1998). Toward a Global Science. Indiana University Press. पृ॰ 126. आई॰ऍस॰बी॰ऍन॰ 9780253333889. मूल से 19 सितंबर 2014 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ Donald Knuth (1997). The Art of Computer Programming: Fundamental Algorithms. Addison-Wesley. पपृ॰ 79–86. आई॰ऍस॰बी॰ऍन॰ 9780201896831. मूल से 19 सितंबर 2014 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ Sigler, Laurence E. (trans.) (2002). Fibonacci's Liber Abaci. स्प्रिंगर-Verlag. आई॰ऍस॰बी॰ऍन॰ 0-387-95419-8. अध्याय II.12, पृ. 404-405.
- ↑ Knott, Ron. "Fibonacci's Rabbits". University of Surrey Faculty of Engineering and Physical Sciences. मूल से 10 जनवरी 2015 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ आधुनिक परंपरा के अनुसार, अनुक्रम F 0=0 के साथ शुरू होता है. लाइबर एबेकी ने प्रारंभिक 0 को छोड़ते हुए,F 1 = 1 के साथ अनुक्रम की शुरूआत की और अभी भी कुछ लोग अनुक्रम को इसी तरह से लिखते हैं.
- ↑ वेबसाइट http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibtable.html Archived 2018-03-14 at the वेबैक मशीन में पहले 300 Fn अभाज्य संख्याओं के रूप में गुणन किया गया है और अधिक व्यापक तालिकाओं से जुड़ा है.
- ↑ Kepler, Johannes (1966). A New Year Gift: On Hexagonal Snow. Oxford University Press. पृ॰ 92. आई॰ऍस॰बी॰ऍन॰ 0198581203. स्ट्रेना स्यु डे निवे सेक्सांगुला (1611)
- ↑ अ आ ई.डब्ल्यू. दिजक्स्त्रा (1978). फाइबोनैचि के सम्मान में. रिपोर्ट EWD654 Archived 2009-10-07 at the वेबैक मशीन
- ↑ Posamentier, Alfred (2007). The (Fabulous) FIBONACCI Numbers. Prometheus Books. पपृ॰ 305. आई॰ऍस॰बी॰ऍन॰ 978-1-59102-475-0. नामालूम प्राचल
|coauthors=की उपेक्षा की गयी (|author=सुझावित है) (मदद) - ↑ एम. मोबियस, Wie erkennt man eine Fibonacci Zahl?, मैथ. सेमेस्टरबर. 1998 (45), 243-246
- ↑ Vorobiev, Nikolaĭ Nikolaevich (2002). "Chapter 1". Fibonacci Numbers. Birkhäuser. पपृ॰ 5–6. आई॰ऍस॰बी॰ऍन॰ 3-7643-6135-2. नामालूम प्राचल
|coauthors=की उपेक्षा की गयी (|author=सुझावित है) (मदद) - ↑ अ आ इ एरिक डब्ल्यू वेइसटीन, मैथवर्ल्ड पर Fibonacci Number
- ↑ "ज्यामिति केंद्र में उल्लेखनीय संख्या 1/89". मूल से 14 दिसंबर 2009 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ एरिक डब्ल्यू वेइसटीन, मैथवर्ल्ड पर Fibonacci Prime
- ↑ J H E Cohn (1964). "Square Fibonacci Numbers Etc". Fibonacci Quarterly. 2: 109–113.
- ↑ ए. पेथो, डायोफंटाइन प्रापर्टिज़ ऑफ़ लीनियर रिकर्सिव सीक्वेंसस II, एक्टा मैथ .Paedagogicae Nyíregyháziensis, 17 (2001), 81-96.
- ↑ वाई. ब्युगॉड, एम. मिग्नोट, एस. सिकसेक: क्लासिकल एंड मॉड्यूलार अप्रोचस टू एक्सपोनेनशल डायोफंटाइन इक्वेशन्स. I. फाइबोनैचि और लुकास परफेक्ट पवर्स. एन. ऑफ़ मैथ. (2), 163 (2006), 969-1018.
- ↑ रॉस होन्सबर्गर मैथमेटिकल जेम्स III (एएमएस डोलशियानी मैथमेटिकल एक्सपोसिशन्स नं. 9), 1985, ISBN 0-88385-318-3, पृ. 133.
- ↑ पाउलो रिबेनबोइम, माई नंबर्स, माई फ़्रेंड्स, स्प्रिंगर-वेरलाग 2000
- ↑ सु, फ्रांसिस ई., एट अल. "फाइबोनैचि GCDस प्लीज़." Archived 2009-12-14 at the वेबैक मशीन मड मैथ फ़न फ़ैक्ट्स.
- ↑ पाउलो रिबेनबोइम (1996), द न्यू बुक ऑफ़ प्राइम नंबर रिकॉर्ड्स, न्यूयॉर्क: स्प्रिंगर, ISBN 0-387-94457-5, पृ. 64
- ↑ फ्रैंज़ लेम्मेरमेयर (2000), रेसिप्रोसिटी लॉस, न्यूयॉर्क: स्प्रिंगर, ISBN 3-540-66957-4, एक्स 2.25-2.28, पृ. 73-74
- ↑ लेम्मरमेयर, एक्स. 2.28, पृ. 73-74
- ↑ लेम्मरमेयर, एक्स. 2.27 पृ. 73
- ↑ वेबसाइट http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibtable.html Archived 2018-03-14 at the वेबैक मशीन पहले 300 फाइबोनैचि अभाज्य संख्याओं का गुणनखंड करना.
- ↑ Knuth, Donald E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd संस्करण). Addison-Wesley. आई॰ऍस॰बी॰ऍन॰ 0-201-89683-4. (पृ. 343)
- ↑ M. Avriel and D.J. Wilde (1966). "Optimality of the Symmetric Fibonacci Search Technique". Fibonacci Quarterly (3): 265–269.
- ↑ अमिगा ROM कर्नेल रेफ़रेन्स मैनुअल, एडिसन-वेसले 1991
- ↑ "IFF - मल्टीमीडियाविकी". मूल से 30 दिसंबर 2009 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ "फाइबोनैचि संख्या निरूपण का एक अनुप्रयोग". मूल से 25 नवंबर 2009 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ "अनुक्रम का एक व्यावहारिक प्रयोग". मूल से 30 मई 2008 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ "ज़ेकेनडोर्फ़ निरूपण". मूल से 3 अक्तूबर 2009 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ S. Douady and Y. Couder (1996). "Phyllotaxis as a Dynamical Self Organizing Process" (PDF). Journal of Theoretical Biology. 178 (178): 255–274. आइ॰एस॰एस॰एन॰ 0022-5193. डीओआइ:10.1006/jtbi.1996.0026. मूल (PDF) से 26 मई 2006 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ Jones, Judy (2006). "Science". An Incomplete Education. Ballantine Books. पपृ॰ 544. आई॰ऍस॰बी॰ऍन॰ 978-0-7394-7582-9. नामालूम प्राचल
|coauthors=की उपेक्षा की गयी (|author=सुझावित है) (मदद) - ↑ A. Brousseau (1969). "Fibonacci Statistics in Conifers". Fibonacci Quarterly (7): 525–532.
- ↑ "Marks for the da Vinci Code: B–". Computer Science For Fun: CS4FN. मूल से 31 मई 2009 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
- ↑ Prusinkiewicz, Przemyslaw (1989). Lindenmayer Systems, Fractals, and Plants (Lecture Notes in Biomathematics). स्प्रिंगर-Verlag. आई॰ऍस॰बी॰ऍन॰ 0-387-97092-4. नामालूम प्राचल
|coauthors=की उपेक्षा की गयी (|author=सुझावित है) (मदद) - ↑ Vogel, H (1979), "A better way to construct the sunflower head", Mathematical Biosciences, 44 (44): 179–189, डीओआइ:10.1016/0025-5564(79)90080-4
- ↑ Prusinkiewicz, Przemyslaw (1990). [[The Algorithmic Beauty of Plants]]. स्प्रिंगर-Verlag. पपृ॰ 101–107. आई॰ऍस॰बी॰ऍन॰ 978-0387972978. मूल से 19 मई 2007 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009. नामालूम प्राचल
|coauthors=की उपेक्षा की गयी (|author=सुझावित है) (मदद); URL–wikilink conflict (मदद) - ↑ "फाइबोनैचि संख्या और मधुमक्खियों की वंशावली". मूल से 1 मार्च 2012 को पुरालेखित. अभिगमन तिथि 18 नवंबर 2009.
बाहरी कड़ियाँ
संपादित करें- क्या है फिबोनाची नंबरों का जादू
- कुदरत के रंग गणित के संग (पूनम मिश्र)
- फिबोनाचिः फिबोनाचिश्रेणिश्च
- पूर्णांक अनुक्रमों के ऑन-लाइन विश्वकोश में फाइबोनैचि संख्या अनुक्रमA000045
- मैथपेजस पर फाइबोनैचि अनुक्रम Mod m के आवर्तक
- फाइबोनैचि अनुक्रमों का अव्यवस्थित व्यवहार
- वैज्ञानिकों द्वारा प्रकृति में फाइबोनैचि सर्पिल घुमाव के गठन का सुराग पाना


