त्रिकोणमितीय फलन
| यह लेख मुख्य रूप से अथवा पूर्णतया एक ही स्रोत पर निर्भर करता है। कृपया इस लेख में उचित संदर्भ डालकर इसे बेहतर बनाने में मदद करें। |
गणित में त्रिकोणमितीय फलन (trigonometric functions) या 'वृत्तीय फलन' (circular functions) कोणों के फलन हैं। ये त्रिभुजों के अध्ययन में तथा आवर्ती संघटनाओं (periodic phenomena) के मॉडलन एवं अन्य अनेकानेक जगह प्रयुक्त होते हैं।
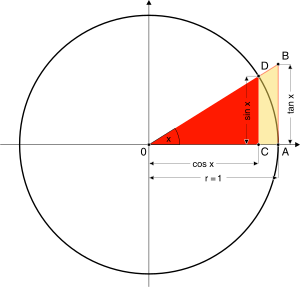
ज्या (sine), कोज्या (कोज) (cosine) तथा स्पर्शज्या (स्पर) (tangent) सबसे महत्व के त्रिकोणमितीय फलन हैं। ईकाई त्रिज्या वाले मानक वृत्त के संदर्भ में ये फलन सामने के चित्र में प्रदर्शित हैं। इन तीनों फलनों के व्युत्क्रम फलनों को क्रमशः व्युज्या (व्युज) (cosecant), व्युकोज्या (व्युक) (secant) तथा व्युस्पर्शज्या (व्युस) (cotangent) कहते हैं।
समकोण त्रिभुज परा आधारित परिभाषाएँ
संपादित करें- संकेत
सामने = कोण सामने की भुजा की लम्बाई
संलग्न = कोण से संलग्न (लगी हुई) भुजा की लम्बाई
कर्ण = समकोण त्रिभुज का विकर्ण
कुछ विशिष्ट कोणों के त्रिकोणमित्तिय फलनों के मान
संपादित करें| फलन | |||||||
|---|---|---|---|---|---|---|---|
| ज्या | |||||||
| कोज्या | |||||||
| स्पर्शज्या | अपरिभाषित[1] | ||||||
| व्युस्पर्शज्या | अपरिभाषित[1] | ||||||
| व्युकोज्या | अपरिभाषित[1] | ||||||
| व्युज्या | अपरिभाषित[1] |
निम्नलिखित सारणी में यह दिखाया गया है कि चारों चतुर्थांशों के कोणों के लिये त्रिकोणमितीय फलनों के चिह्न क्या होते हैं।
| चतुर्थांश (Quadrant) | ज्या तथा व्युज्या | कोज्या तथा व्युकोज्या | स्पर्शज्या तथा व्युस्पर्शज्या |
|---|---|---|---|
| I | + | + | + |
| II | + | − | − |
| III | − | − | + |
| IV | − | + | − |
ग्राफ
संपादित करेंपरस्पर संबन्ध
संपादित करेंत्रिकोणमितीय फलन निम्नलिखित तालिका में दिये गये सम्बन्धों द्वारा परस्पर बदले जा सकते हैं-
| ज्या | कोज्या | स्पर्शज्या | व्युस्पर्शज्या | व्युकोज्या | व्युज्या | |
|---|---|---|---|---|---|---|
| ज्या (x) | ||||||
| कोज (x) | ||||||
| स्पर (x) | ||||||
| व्युस (x) | ||||||
| व्युक (x) | ||||||
| व्युज (x) |
त्रिकोणमितीय फलनों का अनन्त श्रेणी के रूप में विस्तार
संपादित करेंत्रिकोणमितीय फलनों का इतिहास
संपादित करेंआर्यभट्ट के सूर्यसिद्धान्त में 'ज्या' तथा 'कोटिज्या' का प्रयोग हुआ है जो क्रमशः sine व cosine के समानार्थी हैं। भारत से यह ज्ञान अरबों के पास गया और फिर यूरोप को गया।
आज प्रयोग किये जाने वाले सभी छः त्रिकोणमितीय फलन ९वीं शती तक इस्लामी गणित में प्रयोग होने लगे थे। अल-ख्वारिज्मी ने ज्या, कोज्या और स्पर्शज्या की सारणियाँ बनायी थी।
संगमग्राम के माधव ने पंद्रहवीं शदी के आरम्भ में त्रिकोणमितीय फलनों का का अध्ययन श्रेणी के रूप में किया है।
सन्दर्भ
संपादित करेंइन्हें भी देखें
संपादित करें- प्रतिलोम त्रिकोणीमितीय फलन या प्रतिलोम वृत्तीय फलन (Inverse trigonometric functions)
- हाइपरबोलिक फलन
- ज्या, कोटिज्या और उत्क्रमज्या का इतिहास
बाहरी कड़ियाँ
संपादित करें- Visionlearning Module on Wave Mathematics
- GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions
- Dave's draggable diagram. (Requires java browser plugin)